Energía Cinética y Potencia

Energía Cinética


Cuando un cuerpo está en movimiento posee energía cinética ya que al chocar contra otro puede moverlo y, por lo tanto, producir un trabajo.

Para que un cuerpo adquiera energía cinética o de movimiento, es decir, para ponerlo en movimiento, es necesario aplicarle una fuerza. Cuanto mayor sea el tiempo que esté actuando dicha fuerza, mayor será la velocidad del cuerpo y, por lo tanto, su energía cinética será también mayor.

Otro factor que influye en la energía cinética es la masa del cuerpo.

Por ejemplo, si una bolita de vidrio de 5 gramos de masa avanza hacia nosotros a una velocidad de 2 km / h no se hará ningún esfuerzo por esquivarla. Sin embargo, si con esa misma velocidad avanza hacia nosotros un camión, no se podrá evitar la colisión.

La fórmula que representa la Energía Cinética es la siguiente:

E c = 1 / 2 · m · v²

E c = Energía cinética

m = masa

v = velocidad

Cuando un cuerpo de masa m se mueve con una velocidad v posee una energía cinética que está dada por la fórmula escrita más arriba.

En esta ecuación, debe haber concordancia entre las unidades empleadas. Todas ellas deben pertenecer al mismo sistema. En el Sistema Internacional (SI), la masa m se mide en kilogramo (kg) y la velocidad v en metros partido por segundo ( m / s), con lo cual la energía cinética resulta medida en Joule ( J ).

---

Potencia

La potencia es la cantidad de trabajo efectuado por unidad de tiempo. Esto es equivalente a la velocidad de cambio de energía en un sistema o al tiempo empleado en realizar un trabajo, según queda definido por:



Donde

* P es la potencia.
* E es la energía total o trabajo.
* t es el tiempo.

Potencia mecánica es el trabajo realizado por una máquina o una persona en un determinado intervalo de tiempo.

Fuentes:

• Profesor en Línea.cl
  
• Potencia - Wikipedia

Leer Más...

Resumen

Energía y Potencia

Escaneado desde: Física de Alberto G. Heinemann. Editorial: Estrada

Leer Más...

Resumen

Problemas sobre Trabajo, Energía y Potencia

Problema n° 1) Transformar 250 kgf.m a Joul y kW.h.

Problema n° 2) ¿Cuántos kgf.m y Joul representan 25 kW.h?.

Problema n° 3) Indicar cuántos Joul y kW.h son 125478 kgm.

Problema n° 4) Indicar el trabajo necesario para deslizar un cuerpo a 2 m de su posición inicial mediante una fuerza de 10 N.

Problema n° 5) ¿Qué trabajo realiza un hombre para elevar una bolsa de 70 kgf a una altura de 2,5 m?. Expresarlo en:

a) kgf.m
b) Joule
c) kW.h

Problema n° 6) Un cuerpo cae libremente y tarda 3 s en tocar tierra. Si su peso es de 4 N, ¿qué trabajo deberá efectuarse para elevarlo hasta el lugar desde donde cayo?. Expresarlo en:

a) Joule.
b) kgm.

---

Problema nº 1)

Desarrollo
1 kgf.m ® 9,807 J
250 kgf.m ® x = 250 kgf.m × 9,807 J/1 kgf.m

x = 2451,75 J

1 W = 1 J/s
1kW = 1.000 J/s
1kW.h = 1.000 J.3.600 s/s
1kW.h = 3.600.000 J s/s
1 J = 1kW.h/3.600.000

1 kgf.m ® 9,807 J/3.600.000
250 kgf.m ® x = 250 kgf.m × 9,807 J/3.600.000 kgf.m

x = 6,81.10-4 kW.h

---

Problema nº 2)

Desarrollo
1 kW.h ® 3.600.000 J
25 kW.h ® x = 25 kW × 3.600.000 J/1 kW.h

x = 9.107 J

1 kW.h ® 3.600.000 kgf.m/9.807
25 kW.h ® x = 25 kW.h × 9,807 × 3.600.000 J/1 kW.h

x = 9.177.118 kgf.m

---

Problema nº 3)

Desarrollo
1 kgf.m ® 9,807 J
125.478 kgf.m ® x = 125.478 kgf.m × 9,807 J/1 kgf.m

x = 1.230.563 J

1 kgf.m ® 9,807 J/3.600.000
125.478 kgf.m ® x = 125.478 kgf.m × 9,807 J/3.600.000 kgf.m

x = 0,3418 kW.h

---

Problema nº 4)

Desarrollo
L = F × d
L = 10 N × 2 m

L = 20 J

---

Problema nº 5)

Desarrollo
a)

L = F × d
L = 70 kgf × 2,5 m
L = 175 kgf.m

b)

L = 175 kgf.m × 9,807 J/kgf.m
L = 1716,225 J

c)

L = 175 kgf.m × 9,807 J/3.600.000 kgf.m
L = 0,000477 kW.h

---

Problema nº 6)

Desarrollo
L = F.d

En éste caso se trata de la fuerza peso, por lo tanto:

L = P.d

y al ser un movimiento vertical la distancia es la altura:

L = P.h

Mediante cinemática calculamos la altura para caída libre.

h = ½.g.t ²

h = ½ × 9,807 (m/s ²) × (3 s) ²
h = ½ × 9,807 (m/s ²) × 9 s ²
h = 44,1315 m

Luego:

a)

L = P × h
L = 4 N × 44,1315 m
L = 176,526 J

b)

L = 176,526 J/(9,807 kgf.m × J)
L = 18 kgf.m


Fuente: FísicaNet.com.ar

Leer Más...

Resumen

Problemas sobre Trabajo, Energía y Potencia Parte 2

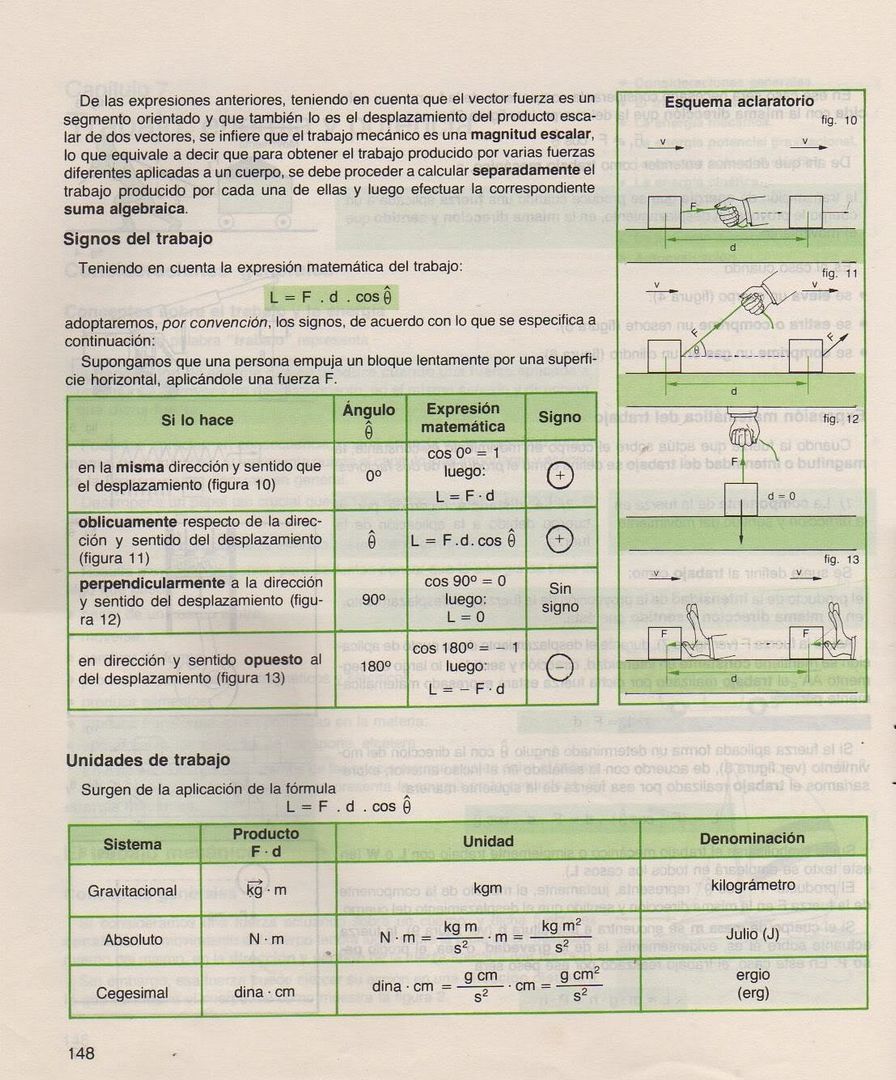
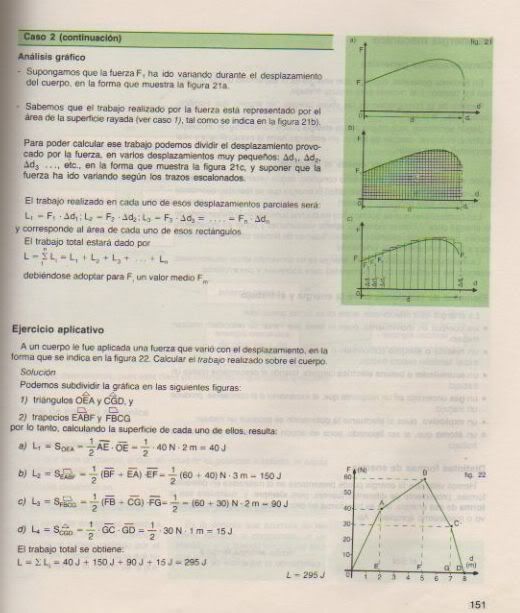
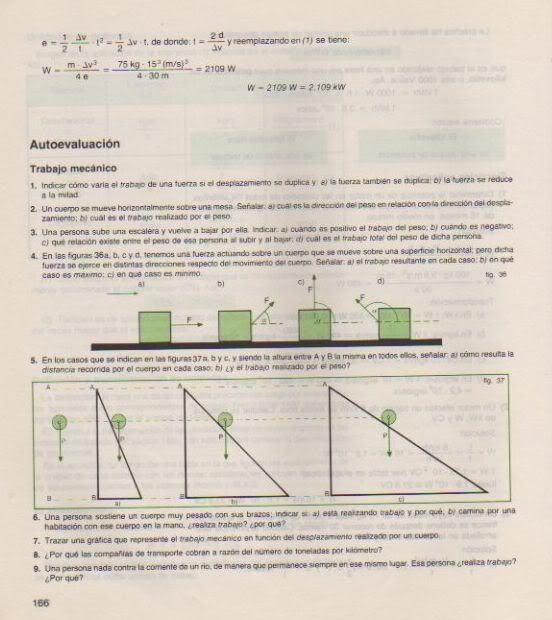
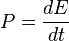Problema n° 1) Un proyectil que pesa 80 kgf es lanzado verticalmente hacia arriba con una velocidad inicial de 95 m/s. Se desea saber:

a) ¿Qué energía cinética tendrá al cabo de 7 s?.

b) ¿Qué energía potencial tendrá al alcanzar su altura máxima?.

Problema n° 2) ¿Qué energía cinética alcanzará un cuerpo que pesa 38 N a los 30 s de caída libre?.

Problema n° 3) ¿Qué energía cinética alcanzará un cuerpo de masa 350 kg si posee una velocidad de 40 m/s?.

Problema n° 4) ¿Con qué energía tocará tierra un cuerpo que pesa 2500 g si cae libremente desde 12 m de altura?.

Problema n° 5) Un cuerpo de 200 N se desliza por un plano inclinado de 15 m de largo y 3,5 de alto, calcular:

a) ¿Qué aceleración adquiere?.

b) ¿Qué energía cinética tendrá a los 3 s?.

c) ¿Qué espacio recorrió en ese tiempo?.

Problema n° 6) ¿Qué energía potencial posee un cuerpo de masa 5 kg colocado a 2 m del suelo?.

Problema n° 7) Si el cuerpo del ejercicio anterior cae, ¿con qué energía cinética llega al suelo?.

Problema n° 8) Sabiendo que cada piso de un edificio tiene 2,3 m y la planta baja 3 m, calcular la energía potencial de una maceta que, colocada en el balcón de un quinto piso, posee una masa de 8,5 kg.

Problema n° 9) Un cuerpo de 1250 kg cae desde 50 m, ¿con qué energía cinética llega a tierra?.

Problema n° 10) Un proyectil de 5 kg de masa es lanzado verticalmente hacia arriba con velocidad inicial de 60 m/s, ¿qué energía cinética posee a los 3 s? y ¿qué energía potencial al alcanzar la altura máxima?.

---

Problema nº 1)
Desarrollo
Datos:

P = 80 kgf

v₀ = 95 m/s

t = 7 s

a) Mediante cinemática calculamos la velocidad luego de 7 s:

vf = v₀ - g.t

vf = 95 m/s + (- 9,807 m/s ²).7 s
vf = 95 m/s - 68,649 m/s
vf = 26,351 m/s

Luego:

Ec = ½.m.v ²

La masa es:

m = 80 kg

Ec = ½.80 kg.(26,351 m/s) ²

Ec = 27775,01 J

b) Mediante cinemática calculamos la altura máxima:

vf ² - v₀ ² = 2.g.h

- v0 ²/2.g = h

h = (95 m/s) ²/(2.9,807 m/s ²)
h = 460,13 m

Con éste dato hallamos la energía potencial:

Ep = m.g.h

Ep = 80 kg.9,807 (m/s ²).460,13 m

Ep = 361.000 J

Pero mucho mas simple es sabiendo que la energía potencial cuando se anula la velocidad es igual a la energía cinética inicial (si no hay pérdidas):

Ec₁ = Ep2

Ec₁ = ½.m.v1 ²
Ec = ½.80 kg.(95 m/s) ²

Ec₁ = 361.000 J = Ep2

---

Problema nº 2)
Desarrollo
Datos:

P = 38 N

t = 30 s

Calculamos la velocidad:

vf = g.t
vf = 9,807 (m/s ²).30 s
vf = 294,21 m/s

Con éste dato calculamos la energía cinética:

Ec = ½.m.v ²
Ec = ½.(38 N/9,807 m/s ²).(294,21 m/s) ²

Ec = 167.700 J

---

Problema nº 3)

Desarrollo
Ec = ½.m.v ²
Ec = ½.350 kg.(40 m/s) ²

Ec = 280.000 J

---

Problema nº 4)

Desarrollo
Si cae libremente su velocidad inicial es nula, por lo tanto toda su energía potencial (dada por la altura) se convertirá en energía cinética:

Ec₂ = Ep₁

Ep₁ = m.g.h

Ep₁ = 2,5 kg.9,807 (m/s ²).12 m

Ep₁ = 294,21 J = Ec₂

---

Problema nº 5)
Desarrollo
Datos:

P = 200 N

l = 15 m

h = 3,5 m

t = 3 s



a) En el eje "x":

Σ Fx = m.a

Px = m.a

pero:

Px = P.sen α

m.a = P.sen α

m.a = m.g.sen α

a = g.sen α

Por otra parte:

sen α = 3,5 m/15 m = 0,233

a = 9,807 (m/s ²).0,233

a = 2,29 m/s ²

b) Suponiendo que parte del reposo:

vf = a.t

luego:

Ec = ½.m.vf ²
Ec = ½.m.(a.t) ²

Ec = ½.(200 N/9,807 m/s ²).(2,29 m/s ².3 s) ²

Ec = 480,54 J

c)

e = ½.a.t ²

e = ½.2,29 m/s ².(3 s) ²

e = 10,29 m

---

Problema nº 6)

Desarrollo
Ep = m.g.h
Ep = 5 kg.9,807 (m/s ²).2 m
Ep = 98,07 J

---

Problema nº 7)

Desarrollo
Si no hubo pérdidas por rozamiento, toda la energía potencial se transformó en energía cinética:

Ec = 98,07 J

---

Problema nº 8)

Desarrollo
h = 2,3 m.4 + 3 m = 14,5 m

El balcón del 5° piso es el techo del 4° piso

Ep = m.g.h
Ep = 8,5 kg.9,807 (m/s ²).14,5 m
Ep = 1017 J

---

Problema nº 9)

Desarrollo
Recordemos que toda la energía potencial se transforma en energía cinética:

Ep₁ = Ec₂

Ep₁ = Ec₂ = m.g.h₁
Ep₁ = 1250 kg.9,807 (m/s ²).50 m
Ep = 612.937,5 J

---

Problema nº 10)

Desarrollo
Primero hallamos la velocidad a los 3 s del lanzamiento:

v₂ = v₁ + g.t

v₂ = 60 m/s + (- 9,807 m/s ²).3 s

v₂ = 30,579 m/s

Luego calculamos la energía cinética:

Ec₂ = ½.m.v2 ²
Ec₂ = ½.5 kg.(30,579 m/s) ²
Ec₂ = 2.337,69 J

Para la segunda parte debemos tener en cuenta que cuando alcanza la altura máxima la velocidad se anula, por lo tanto, toda la energía cinética inicial se transformó en energía potencial:

Ec₁ = ½.m.v₁ ²
Ec₁ = ½.5 kg.(60 m/s) ²
Ec₁ = 9.000 J

Ep₂ = 9.000 J


Fuente: FísicaNet.com.ar

Leer Más...

Resumen

Videos

Leer Más...

Resumen